Aksonometria ukośna z zadanym kierunkiem rzutowania
Obecny model to pochodna poprzedniego - nazwany przez nas "aksonometria ukośna-prosta".
Różnica polega na uszczegółowieniu parametrów :
skala i ∠α.
∠α będzie decydował o "skali" zaś ∠β to kąt pod jakim narysujemy oś OY
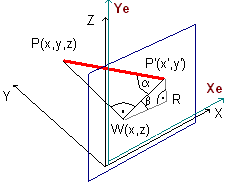
Charakterystyka modelu to kierunek rzutu określony przez dwa kąty:
α i β - patrz rysunek powyżej.
Rysunek wykonamy w płaszczyżnie XZ.
Z Δ WPP' obliczmy :
| WP'=y·ctgα |
|
xe=x+WP'·cosβ = x+y·ctgα·cosβ ye=z+WP'·sinβ = z+y·ctgα·sinβ |
Poprawimy jeszcze procedurę rysującą odcinek w przestrzeni:
W zaleznosci od wartosci parametru α i β wyróznia sie kilka typowych
rzutów ukosnych.
Dla α=45º i β∈{30º,45º} - rzut kawaleryjski
dla α=63,4º i β∈{30º,45º} - rzut gabinetowy
W aplecie ilustrującym ten model, możliwość zmiany kątów α i β pozwala jedynie zorientować się jak może być prezentowana bryła. Poza czysto estetycznymi aspektami, nie można dodatko interpretować stanów bryły (np położenie obserwatora, bryły).