Aksonometria ukośna "prosta"
Skorzystamy z twierdzenie K. Pohlkego (1853 r)
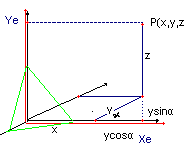
Skorzystamy z tego twierdzenia. Załóżmy, że mamy punkt przestrzeni P(x,y,z) (patrz rysunek niżej).
Rzutnią aksonometryczną będzie płaszczyzna trójkąta (kolor zielony) - ale ekran komputera umieszczony w płaszczyżnie XY. Aplet po lewej stronie jest implementacją tego modelu.
Ten model charakteryzuje deformacja liniowa 1:skala:1 oraz kąt α pod jakim rysujemy oś Y.
W praktyce często przyjmuje się :
skala=½ i α=45º.
Tak przyjeto w powyższym przykładzie.
Mamy narysować taką właśnie scenę tzn mając współrzędne przestrzenne (x,y,z) , szukamy pary współrzędnych ekranowych (xe,ye). Ale oto wzory (patrz rysunek po prawej) A(x,y,z)=(xe,ye):
xe=x+y·skala·cosα
ye=z+y·skala·sinα
Zaletą modelu jest jego prostota, wadą problem z ustaleniem kierunku rzutowania.. Sensownym wydaje się, by projekcję bryły zmieniać jedynie stosując wzory na obrót punktu w przestrzeni. Dynamiczna zmiana któregokolwiek z parametrów modelu (tzn skala lub α) jedynie wprowadza chaos w obserwacji.
Jeśli potrafisz rysować linię w przestrzeni 2-wymiarowej i jest to np procedura linia(g,Pkt p, Pkt k) , wtedy analogiczna Pkt3d.linia(g,Pkt p, Pkt k) w naszym modelu przyjmuje postać :
Informacje o wierzchołkach bryły (np graniastosłupa o podstawie wielokąta foremnego) możemy zgromadzić np w tablicy w typu Pkt3d, zaś narysowanie bryły jest już proste :
public void graniastoslup(int n,double r,double h) | public void rysuj(Graphics g) |
{
double fi=2*Math.PI/n;
for(int i = 0; i <= n-1; i++)
{
w[i].war(r*Math.cos(i*fi),r*Math.sin(i*fi),-h/2);
w[i+n].war(w[i].x,w[i].y,h/2);
}
}
|
{int i;
for(i = 0;i < n; i++)
{
Pkt3d.linia(g,w[i],w[(i+1)%n]);
Pkt3d.linia(g,w[i+n],w[n+(i+1)%n]);
Pkt3d.linia(g,w[i],w[i+n]);
}
}
|