Okrąg i jego równanie parametryczne

(3kB)

Bardzo upraszczając, równanie opisujące daną figurę, to wzór pozwalający wyznaczyć współrzędne wszystkich jej punktów. Równanie okręgu jest bardzo znane :
x2 + y2=r2
 a jeśli środek okręgu ma współrzędne w punkcie (a, b) to uzyskujemy postać :
(x - a)2 +( y - b)2=r2

W informatyce niezwykle chętnie posługujemy się równaniem parametrycznym. Z dwóch powodów:

  1. dla równania parametrycznego wygodnie definiuje się algorytm rysujący
  2. wygodnie rysuje się część figury, tu łuk okręgu

Jakie jest zatem równanie parametryczne okręgu ?
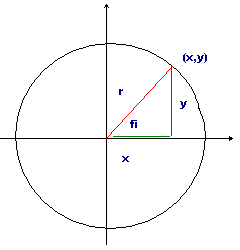
  x=r·cos(fi);
  y=r·sin(fi);
Równanie takie często zapisuje się tak : [ r·cos(fi) , r·sin(fi) ]
A oto algorytmy rysujące :


Pascal
Java
 Procedure Okrag(a,b,r:real)
var x,y,kat :real;
begin
   kat:=0;
   Repeat
       x:=a+r*cos(kat);
       y:=b+r*sin(kat);
       Punkt(a,b);
       kat:=kat+delta;
   Until kat>2*PI;
end;

  public void okrag(Graphics g,double a,double b,double r)
       }
            double kat,x,y;
            g.setColor(Color.red);
            kat=0;
          do
            {
                 x=a+r*Math.cos(kat);
                y=b+r*Math.sin(kat);
                Punkt(g,x,y);
                kat+=delta;
            }
          while ( kat<(2*Math.PI) );
       }

Z racji oczywistych rozwiązanie, w zasadzie nie ma praktycznego zastosowania w procedurach rysujących okrąg ( z wielu powodów ). Zobaczmy prostą implementację tego rozwiązania :

Powinna jednak pobudzić naszą wyobraźnię...