Foremne figury Sierpińskiego
 Z Wikipedii
Z Wikipedii
Trójkąt Sierpińskiego (znany też jako uszczelka Sierpińskiego) jest jednym z najprostszych fraktali, znanym na długo przed powstaniem tego pojęcia ...
Ciekawym algorytmem pozwalającym otrzymać trójkąt Sierpińskiego jest gra w chaos. Narysujmy trzy punkty A, B i C tak, żeby nie leżały na jednej prostej. Wybierzmy dowolny punkt D, leżący wewnątrz trójkąta ABC (Możemy wybrać także punkt spoza wnętrza trójkąta, wtedy kilka pierwszych punktów nie będzie należała do Trójkąta Sierpińskiego). Następnie należy wielokrotnie powtórzyć następującą operację: losowo wybieramy jeden z punktów A, B lub C, rysujemy punkt w połowie odległości między D i wybranym punktem. Nowo narysowany punkt oznaczamy przez D itd..
Zobacz też notę biograficzną Wacława Sierpińskiego
Na początek prezentacja:
Postąpimy wg tego przepisu, modyfikując go tak, by zastosować nasze ulubione wzory.
Po pierwsze otrzymamy dowolny wielokat foremny Sierpińskiego, tzn uzyskany wg. powyższego algorytmu, po drugie punkt D będziemy rysowali niekoniecznie w połowie odległości między "poprzednim" D i wybranym wierzchołkiem wielokąta. W programie przykładowym będzie oczywiście możliwość ustawienia parametrów tak, by otrzymać klasyczny trójkąt Sierpińskiego.
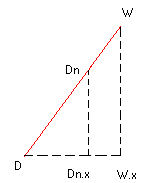
Niech dany będzie wielokąt foremny:
tzn liczba n_kat, promień r
, kąt φ=2· PI / n, punkt D=(D.x , D.y), liczba sk.
Szukamy punktu Dn=(Dn.x , Dn.y)
"Losowy" wierzchołek W=( r · cos( los· φ) , r · sin( los·φ )),
Wspólrzędna Dn.x:
Dn.x=D.x+(W.x-D.x)*sk
Najprostsza wersja procedury rysującej 25000 punktów foremnej figury Sierpińskiego może wygladać tak:
| public void figura(Graphics g) |
{int los,i;
double fi=2*Math.PI/n_kat;
for(i=0;i<25000;i++)
{
los=(int)(Math.random()*n_kat+1);
d.x=d.x+(r*Math.cos(los*fi)-d.x)*sk;
d.y=d.y+(r*Math.sin(los*fi)-d.y)*sk;
punkt(g,a);
}
}
|