Krzywa pogoni - cel stały
Jest to krzywa jaką zakreśla ścigający w pogoni za swoją ofiarą. Przykładem takiej krzywej jest tor jaki zakreśla pies goniący za zającem (inna nazwa - psia krzywa), czy tor myśliwca który ściga wroga, również nowoczesne rakiety poruszają się wzdłuż tej krzywej by uderzyć w cel. Pierwszy tym zagadnieniem zajął się Francuz Pierre Bouguer. W 1732 Bouguer studiował krzywe gonitwy wykazując się głębokim zrozumieniem matematyki...
Pod podanym wyżej adresem można znaleźć wzory matematyczne opisujące takie krzywe.
My jednak chcemy tylko takie krzywe narysować, wystarczy nam prostsza interpretacja. I jak łatwo się domyśleć "nasze" wzory znowu dzielnie się tutaj spiszą w wektorowym przedstawieniu toru ścigajacego.
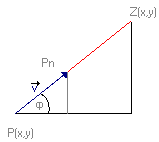
Na rysunku obok jest przedstawiony nasz problem:
punkt P z predkością v porusza się w kierunku punktu Z.
Znamy więc P, Z i v. Podczas rysowania krzywej majac współrzędne punku P będziemy wyliczali współrzędne kolejnego Pn i tak dalej dopóki nie osiągniemy punktu Z
Na poczatku obliczymy φ=ATAN((z.y-p.y)/(z.x-p.x)).
Pn=(p.x + v · cosφ , p.y + v · sinφ)Oczywiście pościg ze stałą prędkością..
Obok najprostsza wersja pościgu : cel jest nieruchomy. Ścigający (pies) tylko na początku ustala kierunek - kat φ
Myszą możesz zmienić położenie punktu docelowego.
Na koniec prosta implementacja rozwiazania. Aby można ją zastosować w praktyce, niezbędne jest wprowadzenie warunków, tak by ruch mógł byc realizowany we wszystkich kierunkach.
| public void do_stalego(Graphics g) |
{ double fi;
fi=Math.atan((z.y-p.y)/(z.x-p.x));
do
{
p.x=p.x+v*Math.cos(fi);
p.y=p.y+v*Math.sin(fi);
punkt(g,p,Color.orange);
}
while(odlegosc(p,z)>Math.abs(v));
}
|