Aksonometria izometryczna-prostopadła

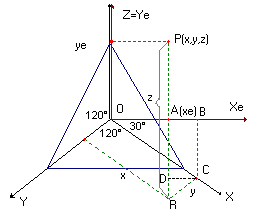
Tym razem w naszym modelu przyjmiemy, że osie aksonometryczne tworzą identyczne katy 120º .
Jeśli przyjąć taką charakterystykę modelu oznacza to trzy znamienne fakty:
  1. skrócenia na wszystkich osiach są identyczne i jak łatwo obliczyć wynoszą √2/3≈0.82.
  2. trójkąt śladów aksonometrycznych jest trójkątem równobocznym ( rzutnia aksonometryczna)
  3. kierunek rzutowania jest prostopadły do trójkąta śladów aksonometrycznych (na rysunku widoczny jako punkt O)


Ekran komputera umieszczamy w płaszczyźnie XeYe.
Obliczymy kolejno :

  1. OB=x·cos 30º
  2. AB=y·cos 30º
  3. xe=OB-AB=x·cos 30º-y·cos 30º=(x-y)·cos 30º
  4. BC=x·sin 30º
  5. DR=y·sin 30º
  6. ye=PR-BC-DR=z-(x+y)·sin 30º
 Ostateczne wzory A(x,y,z)=(xe,ye) 
xe=(x-y)·cos 30º
   ye=z-(x+y)·sin 30º

Poprawimy jeszcze procedurę rysującą odcinek: Pkt3d.linia(g,Pkt p, Pkt k)

linia( g, (p.x-p.y)*ca*skala, p.z-(p.x+p.y)*sa*skala, (k.x-k.y)*ca*skala, k.z-(k .x+k.y)*sa*skala);
gdzie sa=sin 30º oraz ca=cos 30º

A teraz prezentacja bryły w tym modelu.
Przyjęto wymiary i estetykę graniastosłupa dokładnie takie jak w przypadku aksonometrii "prostej", tak by można zauważyć podobieństwa i różnice.