Rzut aksonometryczny
Sceny trójwymiarowe lub po prostu bryły na ekranie komputera przedstawiamy rysując ich rzut.
Zwykle stosuje się rzut środkowy (perspektywa) lub rzut równoległy.
Naszym zadaniem jest wykreślić rzut naszej bryły, wyliczając uprzednio wszystkie jej elementy. W tym celu zastosujemy RZUT AKSONOMETRYCZNY.
 rys. ze strony PK
rys. ze strony PK
"Z internetu (strona Politechniki Koszalińskiej)
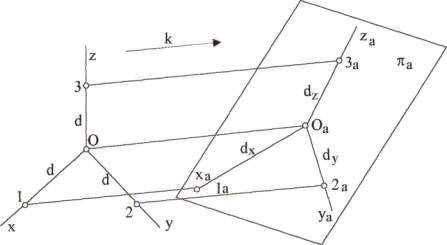
Załóżmy, że dane są trzy osie rzutów x, y i z przecinające się w punkcie O. Odłóżmy od tego punktu na dodatniej części każdej z osi odcinek tej samej długości d przyjęty za jednostkę, po czym rzućmy osie wraz z odcinkami w kierunku k na jakąkolwiek płaszczyznę πa, różną od π1, π2, π3. Płaszczyznę tę nazwiemy rzutnią aksonometryczną.
Otrzymany w ten sposób rzut równoległy będzie figurą składającą się z trzech prostych xa, ya i za mających wspólny punkt Oa i przecinających się pod kątami, których wielkość zależy od ustawienia rzutni aksonometrycznej i od kierunku rzutów.
Na każdej z tych prostych znajdzie się rzut odcinka d (rzuty te oznaczono na rysunku symbolami dx, dy i dz).
Proste xa, ya i za nazywamy osiami aksonometrycznymi, punkt Oa - środkiem aksonometrii, odcinki dx, dy i dz - jednostkami aksonometrycznymi. W przypadku ogólnym nie są one sobie równe, ani nie równają się odcinkowi d,
Stosunki długości odcinków:
dx:d , dy:d , dz:d
nazywamy współczynnikami deformacji liniowej.
I dalej ze strony Politechniki Koszalińskiej : - (rysunek również z tej strony)
|
Cytat
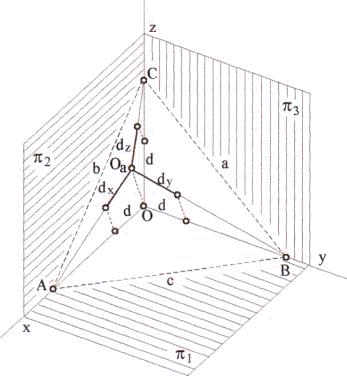
Jeżeli rzutnia aksonometryczna πa nie jest równoległa do żadnej płaszczyzny rzutów, to przecina każdą z osi rzutów odpowiednio w punktach A, B i C.Punkty te są wierzchołkami tzw. trójkąta śladów aksonometrycznych; bokami a, b i c tego trójkąta są odcinki śladów rzutni aksonometrycznej na π1, π2 , π3. Na rysunku wykreślono również osie aksonometryczne wraz z jednostkami aksonometrycznymi; kierunek rzutów jest określony przez prostą OOa. |
Teraz poszukamy analitycznego modelu tego typu przekształceń i zdefiniujemy w miarę prostą implementację, która pozwoli przedstawić na ekranie komputera bryłę (np graniastosłup) .
Jak zwykle postaramy się zastosować "nasz" wzór..