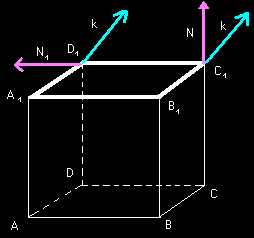
Na rysunku obok pokazano jak roztrzygnięto widoczność ściany.

W dowolnym wierzchołku ściany wystawiamy dwa wektory: normalny (prostopadły do ściany) i wektor kierunku rzutowania (nazwijmy go umownie wektorem obserwacji).

Ściana A₁B₁C₁D₁ jest widoczna
ponieważ <(k,N)<90°

Ściana AA₁D₁D - niewidoczna
ponieważ <(k,N₁)>90°

Krawędzie bryły ocenimy tak:

założymy, że wszystkie są niewidoczne dokonamy przeglądu wszystkich ścian jeśli ściana jest widoczna wszystkie jej krawędzie uznamy za widoczne

Wróćmy do ściany A₁B₁C₁D₁, jest widoczna ponieważ <(k,N)<90°. Oznacza to, że iloczyn skalarny wektorów k i N jest dodatni :

koN=|k|·|N|·cos<(k,N) >0

Dla ściany AA₁D₁D analogiczny iloczyn jest ujemny.

Wektor prostopadły do ściany obliczymy ze wzoru na iloczyn wektorowy a i b
(wektory a i b należą do ściany)

a x b = [ay·bz - by·az , bx·az - ax·bz , ax·by - bx·ay]

Dla oceny widoczności ściany zdefiniujemy następującą funkcję (zakładam, że znam wektor obserwacj):

boolean widoczna(int i,int j,int k) 
{ 
  pkt3d p,q,N; 
  double iloczyn,x,y,z; 

  p=new pkt3d(w[i].x-w[j].x , w[i].y-w[j].y , w[i].z-w[j].z); 
  q=new pkt3d(w[k].x-w[j].x , w[k].y-w[j].y , w[k].z-w[j].z);   
  N=new pkt3d(p.y*q.z-p.z*q.y,p.x*q.z-p.z*q.x,p.x*q.y-p.y*q.x); 
  iloczyn=N.x*obs.x+N.y*obs.y+N.z*obs.z; 
  
  return(iloczyn<0); 
}

Jak łatwo zauważyć, funkcja ocenia jako "widoczna" jeśli wspomniany iloczyn skalarny jest ujemny. Co oznacza, że wektor normalny ściany jest wystawiany "do wnętrza" bryły - sama idea oceny pozostaje bez zmian.

Pozostaje jeszcze ustalić współrzędne wektora obs(x,y,z). Zależą one oczywiście od modelu rzutowania. W rozdziale "Przykład I" zostanie to omówione dokładnie.