Ściany widoczne
Janusz Sobieraj - 28 LO

Widoczność ścian w aksonometrii prostopadłej wg.kierunku obserwacji
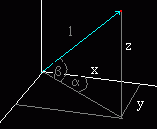Teraz obliczę współrzedne wektora obserwacji (o dł.= 1) w rzucie charakteryzowanym przez kąty kierunku rzutu.
I tak z rysunku otrzumujemy kolejno:
obs.x=cosα·cosβ
obs.y=sinα·cosβ
obs.z=sinβ

Pozostaje "informatyzacja" rozwiązania (problem jest dokładnie ten sam dla obu modeli). Funkcja Widoczna z poprzedniego rozdziału to podstawowe narzędzie.
Pozostaje np wprowadzenie wyniku do metody rzutowanie klasy _3d.

Oto poprawiony fragment kodu klasy _3d oraz procedura oceniejąca widoczność krawędzi: 
public static double sa,ca,sf,cf; 
public static pkt3d obs;  
//--------------------------------------------
public static void rzutowanie(int alfa,int fi) 
{double alfa_=alfa*Math.PI/180; 
  double fi_=fi*Math.PI/180; 

  sa=Math.sin(alfa_); 
  ca=Math.cos(alfa_); 
  sf=Math.sin(fi_); 
  cf=Math.cos(fi_); 

  obs=new pkt3d(cf*sa,cf*ca,sf); 
}

void ocena_Kr(int n) 
{ int i,j; 

  for(i=0;i<=3*n-1;i++) l[i]=false; 

  if (widoczna(2,1,0)) //podstawa dolna
   for(i=0;i<=n-1;i++) l[i]=true; 
    else //>tzn podstawa górna
     for(i=n;i<=2*n-1;i++) l[i]=true; 
  for(i=0;i<=n-1;i++) 
   { 
    j=(i+1)%n; 
    if (widoczna(i+n,i,j)) //ściana boczna
     { 
      l[i]=true; 
      l[2*n+i]=true; 
      l[i+n]=true; 
      l[2*n+j]=true; 
     } 
   } 
}