Funkcje 3D-siatka
Janusz Sobieraj - 28 LO

Jak rysować wykres z=F(x,y) siatką, z "horyzontem"

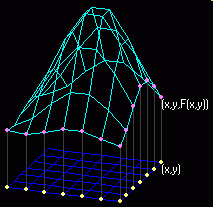
Aplet wykonałem wg pomysłu, który ilustruje rysunek powyżej.
W dziedzinie wyznaczam punkty (x,y) - przecięcia niebieskich linii, dla których obliczam węzły siatki (x,y,f(x,y)). Tak wyznaczone węzły powierzchni funkcji łączę siatką.

Zmienne int ile; double bok określają dziedzinę oraz liczbę węzłów. 
int ile=45; 
double bok=10; 
Punkt[][] w = new Punkt[80][80]; 
void  nalicz_wezly( ) 
{ 
  pkt2d rz=new pkt2d(0,0); 
  double d,x,y,z; 
  d=bok/(double)ile; 
  for(int i=0;i<ile;i++) 
  for(int j=0;j<ile;j++) 
    { 
      x=-bok/2+j*d; 
      y=-bok/2+i*d; 
      z=f(x,y); 
      rz=_3d.rzut(_3d.p3d(kx*x,ky*y,z)); 
      w[i][j].war(lo28.cal_x(rz.x),lo28.cal_y(rz.y)); 
    } 
} 
//-------------------------------------------------------- 
void siatka(Graphics g) 
{int i,j;
  for(i=0;i<getWidth( );i++) 
    {h[i]=getHeight( ); d[i]=0;} 
  for(i=0;i<ile-1;i++) 
    {
    for(j=0;j<ile-1;j++) 
      {
        Odcinek(g,w[i][j],w[i][j+1]); 
        Odcinek(g,w[i][j],w[i+1][j]);
      } 
    Odcinek(g,w[i][ile-1],w[i+1][ile-1]);
    } 
  for(j=0;j<ile-1;j++) 
    Odcinek(g,w[ile-1][j],w[ile-1][j+1]); 
}
Zorganizuję proces tworzenia i rysowania siatki. Zorganizuję tak, by oczywiście uwzględnić tylko widoczne punkty powierzchni. Tu zastosuję znane już rozwiązanie: tablica-horyzont. Horyzont: int[] h=new int[getWidth()];

Odcinki siatki rysuję tak, by każdy jego piksel był oceniany:
widoczny / niewidoczny.
Dlatego w tablicy Punkt w[][] zgromadzę współrzędne węzłów przetworzone do liczb całkowitych.

Same odcinki będę rysował wg znanego algorytmu Bresenhama (opracowany 1963-65 r).

Punkty tworzące Odcinek rysujemy:

void  Kropka(Graphics kt,int x,int y) 
{ 
 if(x>=0&&x<getWidth( )) 
  { 
   if(y<=h[x]) 
    { 
      kt.drawLine(x,y,x,y); 
      h[x]=y; 
    } 
  } 
}

I na koniec kod procedur Kropka i Odcinek razem.