Izometryczna
Janusz Sobieraj - 28 LO

Aksonometria izometryczna-prostopadła

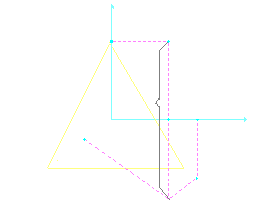
Tym razem w naszym modelu przyjmiemy, że osie aksonometryczne tworzą identyczne katy 120º .
Jeśli przyjąć taką charakterystykę modelu oznacza to trzy znamienne fakty:
  1. skrócenia na wszystkich osiach są identyczne i jak łatwo obliczyć wynoszą √2/3≈0.82.
  2. trójkąt śladów aksonometrycznych jest trójkątem równobocznym ( rzutnia aksonometryczna)
  3. kierunek rzutowania jest prostopadły do trójkąta śladów aksonometrycznych (na rysunku widoczny jako punkt O)


Ekran komputera umieszczamy w płaszczyźnie XeYe.
Obliczymy kolejno :

  1. OB=x·cos 30º
  2. AB=y·cos 30º
  3. xe=OB-AB=x·cos 30º-y·cos 30º=(x-y)·cos 30º
  4. BC=x·sin 30º
  5. DR=y·sin 30º
  6. ye=PR-BC-DR=z-(x+y)·sin 30º
 Ostateczne wzory A(x,y,z)=(xe,ye)
xe=(x-y)·cos 30º
ye=z-(x+y)·sin 30º
Wystarczy teraz poprawić funkcję rzut i procedurę linia

pkt2d rzut(pkt3d p) 
{double x=skala*(p.x-p.y)*ca;
 double y=skala*(p.z-(p.x+p.y)*sa);
  
  return(new pkt2d(x,y; 
}

void linia(Graphics g,pkt3d p,pkt3d k)
{ 
  lo28.linia(g,rzut(p),rzut(k)); 
}
gdzie sa i ca to odpowiednio sinus i cosinus kąta 30º zaś skala=Math.sqrt(2/3);

A teraz prezentacja bryły w tym modelu.
Przyjęto wymiary i estetykę graniastosłupa dokładnie takie jak w przypadku aksonometrii "prostej", tak by można zauważyć podobieństwa i różnice.