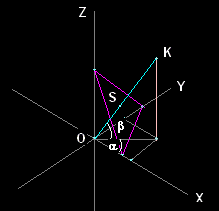
Obok ilustracja tego modelu.
Charakterystyki modelu to kierunek rzutowania, określony przez dwa kąty:
β - kąt kierunku z płaszczyzną XY
α - kąt rzutu kierunku na płaszczyznę XY z osią X,
oraz położenie rzutni-prostopadła do kierunku.

Trójkąt śladów aksonometrycznych (kolor fioletowy) położony jest zawsze prostopadle do kierunku rzutowania OK.
Punkt S (punkt przebicia trójkąta przez kierunek), to rzut początku układu wspólrzędnych O_a.

Ekran komputera umieszczamy na płaszczyznie trójkąta tak by osie układu X_eY_e przecinały się w punkcie S.
Ale rysujemy jak zwykle..

Podam gotowe wzory tego rzutu A[P(x,y,z)]=(x_e,y_e) :

Dla dociekliwych podaję stosunek współczynników deformacji liniowej boków trójkąta śladów:

pkt2d rzut(pkt3d p) 
{double x=p.y*sa+p.x*ca;
 double y=(p.y*ca-p.x*sa)*sf+p.z*cf;
 
 return(new pkt2d ( x,y); 
} 

void linia(Graphics g,pkt3d p,pkt3d k) 
{ 
 lo28.linia(g,rzut(p),rzut(k)); 
} 

To interesująca projekcja bryły. Przy zmianie kątów: oglądania i podniesienia można odnieść wrażenie, ze to my zmieniamy punkt obserwcji bryły.
Aplet tak jak poprzednio daje możliwość obracania bryły.

Mimo skoplikowania modelu walorem jest możliwość kontrolowania "położenia obserwatora" poprzez zmianę kierunku rzutowania oraz bardzo naturalny wygląd sceny.