Obecny model to pochodna poprzedniego - nazwany przez nas "aksonometria ukośna-prosta". Różnica polega na uszczegółowieniu parametrów : skala i <α.
<α będzie decydował o "skali" zaś <β to kąt pod jakim narysujemy oś OY.

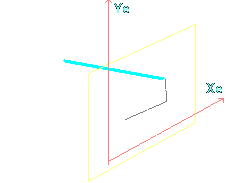
Charakterystyka modelu to kierunek rzutu określony przez dwa kąty: α i β - patrz rysunek powyżej.

Rysunek wykonamy w płaszczyżnie XZ.

Z Δ WPP' obliczmy :

WP'=y·ctgα

Zaś z Δ WRP' mamy wzór rzutu R[P(x,y,z)]=(x',y')=(x_e,y_e):

pkt2d rzut(pkt3d p) 
{ 
  return(new pkt2d(p.x+p.y*ctg*cf , p.z+p.y*ctg*sf)); 
} 
void linia(Graphics g,pkt3d p,pkt3d k) 
{ 
  lo28.linia(g,rzut(p),rzut(k)); 
} 

W zaleznosci od parametru α i β wyróznia sie dwa typowe rzuty ukośne.

1º kawaleryjski α=45º, β:{30º,45º}
2º gabinetowy α=63,4º, β:{30º,45º}

W aplecie ilustrującym ten model, możliwość zmiany kątów α i β pozwala jedynie zorientować się jak może być prezentowana bryła.
Poza czysto estetycznymi aspektami, nie można dodatko interpretować stanów bryły (np położenie obserwatora, bryły). Ekspozycję bryły uzyskujemy obracając ją dookoła osi.