Skorzystamy z tego twierdzenia. Załóżmy, że mamy punkt przestrzeni P(x,y,z) (patrz rysunek niżej).
Rzutnia aksonometryczna bedzie płaszczyzną trójkąt (kolor fioletowy) - ale ekran komputera umieszczony w płaszczyżnie XY. Aplet po lewej stronie jest implementacją tego modelu.

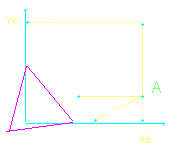
Ten model charakteryzuje deformacja liniowa 1:skala:1 oraz kąt α pod jakim rysujemy oś Y.


W praktyce często przyjmuje się : skala=½ i α=45º. Tak przyjeto w powyższym aplecie.

Zaletą modelu jest jego prostota, wadą problem z ustaleniem kierunku rzutowania.. Sensownym wydaje się, by projekcję bryły zmieniać jedynie stosujac wzory na obrót punktu w przestrzeni. Dynamiczna zmiana któregokolwiek z parametrów modelu (tzn skala lub α) jedynie wprowadza chaos w obserwacji.

pkt2d rzut(pkt3d p) 
{ 
 return(new pkt2d(p.x+skala*p.y*ca,p.z+skala*p.y*sa)); 
} 
//------------------------------------------------------- 
void linia(Graphics g,pkt3d p,pkt3d k) 
{ 
 lo28.linia(g, rzut(p), rzut(k)); 
} 
 

Potrafimy rysowac linie w przestrzeni R² i jest to np procedura lo28.linia(g,pkt2d p, pkt2d k) , wtedy analogiczna procedura w przestrzeni R³ bedzie zrealizowana jak obok.